update

day3/T433080/T433080.md

@@ -0,0 +1,63 @@
+# 快速排序的败北
+
+## 题目背景
+
+小C写出如下快速排序程序：
+```cpp
+int n, a[1005];
+int cnt = 0;
+int partition(int l, int r) {
+    cnt += r-l+1;
+    swap(a[l], a[(l+r)/2]);
+    int i = l+1, j = r, x = a[l];
+    while(1){
+        while(a[i]<x && i<=r) i++;
+        while(a[j]>x && j>=l+1) j--;
+        if(i>=j) break;
+        swap(a[i],a[j]);
+        i++;j--;
+    }
+    swap(a[l],a[j]);
+    return j; 
+}
+
+void qsort(int l, int r){
+    if(l >= r) return;
+    int m = partition(l,r);//分
+    qsort(l,m-1);//解
+    qsort(m+1,r);
+}
+
+int main(){
+	n = 1000;
+   for(int i=1;i<=n;i++) cin>>a[i];
+   qsort(1,n);
+   return 0;
+}
+```
+
+## 题目描述
+
+你做为出题人，想要让小C的快排程序复杂度退化为 $O(n^2)$。
+
+给定整数 $k$，请你构造一组 $n=1000$ 的数据，使得小C的程序运行结束时，计数器 `cnt` 的值超过 $k$。
+
+请认真阅读【评分方式】
+
+## 输入格式
+
+输入1个整数 $k$，代表 `cnt` 要超过的值
+
+## 输出格式
+
+输出一行包含 $n=1000$ 个 `int` 范围整数
+
+## 提示
+
+### 评分方式
+
+共10个测试点，每个测试点10分。
+- 若输入不合法（数字个数少于或者多于 $1000$，格式不对），得 $0$ 分；
+- 否则 `checker` 会执行小C的快排程序并计算 `cnt` 的值，若最终 $cnt>k$ 则得10分、否则得0分。
+
+对于第 $i$ 个测试点，$k=400\times 2^i$。

day3/T490194/T490194.md

@@ -0,0 +1,88 @@
+# 还原排列
+
+## 题目描述
+
+Alice有一个 $0\sim n$ 的排列 $p$，她告诉你 $m$ 条信息，每条信息形如 $(l,r,val)$，表示区间 $[l,r]$ 的 ${\rm mex}$ 值为 $val$。
+- 一个区间的 ${\rm mex}$ 值是最小的没有在这个区间中出现的自然数。
+
+你想要猜出Alice的排列 $p$，或声明无解。
+
+## 输入格式
+
+第一行两个整数 $n$ 和 $m$。
+
+随后 $m$ 行每行三个整数 $l,r,val$ 描述一条信息，表示区间 $[l,r]$ 的 ${\rm mex}$ 值为 $val$。
+
+## 输出格式
+
+如果不存在满足所有条件的排列，输出 $-1$。
+
+否则输出一行 $n+1$ 个正整数，表示一个 $0$ 到 $n$ 的排列。
+
+**本题采用 Special Judge**。如果满足条件的排列有多个，你可以输出任意一个。
+
+## 样例 #1
+
+### 样例输入 #1
+
+```
+3 4
+0 0 0
+0 1 1
+0 2 2
+1 3 3
+```
+
+### 样例输出 #1
+
+```
+3 0 1 2
+```
+
+## 样例 #2
+
+### 样例输入 #2
+
+```
+5 7
+0 1 0
+4 5 0
+1 3 1
+0 5 6
+0 5 6
+2 5 3
+2 3 1
+```
+
+### 样例输出 #2
+
+```
+4 3 5 0 1 2
+```
+
+## 样例 #3
+
+### 样例输入 #3
+
+```
+见下发样例
+```
+
+### 样例输出 #3
+
+```
+
+```
+
+## 提示
+
+对于所有的数据满足：$1 \le n,m\le 5\times 10^5$，$ 0\le l,r\le n$，$0\le val\le n+1$。
+
+- Subtask 1(15 points)：$n,m\le 10$；
+- Subtask 2(20 points)：$n,m\le 20$；
+- Subtask 3(10 points)：$val=0$；
+- Subtask 4(15 points)：排列和区间边界都随机生成；
+- Subtask 5(10 points)：$n\le 10^5$；
+- Subtask 6(30 points)：无特殊限制。
+
+请注意使用效率较高的 IO 方式。

day3/U184510/U184510.cpp

@@ -0,0 +1,6 @@
+#include<bits/stdc++.h>
+using namespace std;
+
+int main(){
+    
+}

day3/U184510/U184510.md

@@ -0,0 +1,117 @@
+# 冒泡排序趟数期望
+
+## 题目背景
+
+Ran很喜欢【冒泡排序】，所以出了很多相关的题目，这又是其中一道。
+
+对于一个排列 $a[1...n]$，进行一趟冒泡排序的代码为：
+```cpp
+for(int i=1;i<n;++i){
+    if(a[i]>a[i+1]) swap(a[i], a[i+1]);
+}
+```
+若排列在 $k$ 趟冒泡排序之后变为有序，则最小的 $k$ 定义为 $res$。
+
+## 题目描述
+
+给一个长度为 $n$ 的随机排列（ $n!$ 种情况等概率出现），请你计算 $res$ 的期望值，对 `1e9+7` 取模。
+
+例如 $n=3$:
+- $a = [1,2,3], res = 0$
+- $a = [1,3,2], res = 1$
+- $a = [2,1,3], res = 1$
+- $a = [2,3,1], res = 2$
+- $a = [3,1,2], res = 1$
+- $a = [3,2,1], res = 2$
+
+期望为 $(0+1+1+2+1+2)/6 = 7/6$
+
+## 输入格式
+
+输入一行1个整数 $n$
+
+## 输出格式
+
+输出1个整数代表答案
+
+## 样例 #1
+
+### 样例输入 #1
+
+```
+3
+```
+
+### 样例输出 #1
+
+```
+166666669
+```
+
+## 样例 #2
+
+### 样例输入 #2
+
+```
+10
+```
+
+### 样例输出 #2
+
+```
+801586487
+```
+
+## 样例 #3
+
+### 样例输入 #3
+
+```
+50
+```
+
+### 样例输出 #3
+
+```
+123038582
+```
+
+## 样例 #4
+
+### 样例输入 #4
+
+```
+12345
+```
+
+### 样例输出 #4
+
+```
+631836361
+```
+
+## 样例 #5
+
+### 样例输入 #5
+
+```
+923456
+```
+
+### 样例输出 #5
+
+```
+276256848
+```
+
+## 提示
+
+对于 20% 的数据，$n\le 8$
+
+对于 40% 的数据，$n\le 16$
+
+对于 60% 的数据，$n \le 3000$
+
+对于 80% 的数据，$n \le 10^5$
+
+对于 100% 的数据，$1\le n\le 10^6$

day3/U184510/chat.md

@@ -0,0 +1,86 @@
+要解决这个问题，我们需要计算一个随机排列需要多少次冒泡排序才能完全有序的期望值。对于这个问题，我们可以采用概率和数学期望的知识进行计算。
+
+### 思路分析
+
+1. **冒泡排序的特性**：
+    - 在每一趟冒泡排序中，至少有一个元素会被移到最终位置。
+    - 因此，一个长度为 `n` 的排列最多需要 `n-1` 趟冒泡排序。
+
+2. **逆序对**：
+    - 冒泡排序的趟数与排列的逆序对数量密切相关。
+    - 一个逆序对 `(i, j)` 满足 `i < j` 且 `a[i] > a[j]`。
+    - 每次冒泡排序至少消除一个逆序对。
+
+3. **期望值计算**：
+    - 我们需要计算的是在随机排列下冒泡排序趟数的期望值。
+    - 设 `E(n)` 为长度为 `n` 的随机排列需要的冒泡排序的期望趟数。
+
+### 数学推导
+
+对于一个长度为 `n` 的随机排列，它的逆序对数量期望为 `n*(n-1)/4`。因为每次冒泡排序消除一个逆序对，逆序对数量减为 0 所需的期望趟数可以看作是期望逆序对数。
+
+### 动态规划优化
+
+1. **定义状态**：
+    - 我们用 `dp[i]` 表示长度为 `i` 的排列需要的期望冒泡排序趟数。
+
+2. **状态转移**：
+    - 对于长度为 `i` 的排列，期望趟数 `dp[i]` 可以由长度为 `i-1` 的排列推导出来，加上在长度为 `i` 的排列上添加一个新的元素后的期望趟数变化。
+
+3. **最终结果**：
+    - 我们需要将结果对 `1e9+7` 取模。
+
+### C++ 实现
+
+以下是求解该问题的 C++ 代码：
+
+```cpp
+#include <iostream>
+#include <vector>
+using namespace std;
+
+const int MOD = 1e9 + 7;
+
+int mod_inv(int a, int m) {
+    int m0 = m, t, q;
+    int x0 = 0, x1 = 1;
+    if (m == 1) return 0;
+    while (a > 1) {
+        q = a / m;
+        t = m;
+        m = a % m, a = t;
+        t = x0;
+        x0 = x1 - q * x0;
+        x1 = t;
+    }
+    if (x1 < 0) x1 += m0;
+    return x1;
+}
+
+int main() {
+    int n;
+    cin >> n;
+
+    vector<long long> dp(n + 1, 0);
+    for (int i = 2; i <= n; ++i) {
+        dp[i] = (dp[i - 1] + (i * (i - 1) / 2) % MOD * mod_inv(i, MOD)) % MOD;
+    }
+
+    cout << dp[n] << endl;
+    return 0;
+}
+```
+
+### 解释
+
+1. **求模逆元**：
+    - 使用扩展欧几里得算法求模逆元。
+
+2. **动态规划**：
+    - `dp[i]` 表示长度为 `i` 的排列需要的期望冒泡排序趟数。
+    - 通过前一状态 `dp[i-1]` 递推得到当前状态 `dp[i]`。
+
+3. **输出结果**：
+    - 最终结果输出 `dp[n]`，即长度为 `n` 的排列所需的期望冒泡排序趟数。
+
+该代码有效地计算了长度为 `n` 的随机排列的期望冒泡排序趟数，并对结果取模 `1e9+7`。

day3/U86432/U86432.md

@@ -0,0 +1,85 @@
+# 捞鱼(fish)
+
+## 题目描述
+
+相信大家做过【Fishes】这题之后对捞鱼都很感兴趣，给1个 $n\times m$ 的鱼池，和一个边长 $r$ 的正方形渔网。鱼池里有 $k$ 条鱼，位置给定。
+
+现在尝试在所有合法位置（渔网必须全部在鱼池内部）撒网，请问能捕到 $x$ 条鱼的位置有多少个，请你输出 $x=0,1,...,k$ 时的所有答案。
+
+## 输入格式
+
+第一行输入4个整数 $n,m,r,k$
+
+接下来 $k$ 行，每行2个正整数 $(x,y)$ 代表1条鱼的位置，可能有重复
+
+## 输出格式
+
+输出 $k+1$ 行，分别代表能捕到 $0,1,...,k$ 条鱼的位置有多少个
+
+## 样例 #1
+
+### 样例输入 #1
+
+```
+3 3 2 3
+2 1
+2 2 
+2 3
+```
+
+### 样例输出 #1
+
+```
+0
+0
+4
+0
+```
+
+## 样例 #2
+
+### 样例输入 #2
+
+```
+1000000000 1000000000 10 4
+1 1
+5000 5000
+5001 5001
+5000 5000
+```
+
+### 样例输出 #2
+
+```
+999999981999999961
+20
+19
+81
+0
+```
+
+## 样例 #3
+
+### 样例输入 #3
+
+```
+见下发样例
+```
+
+### 样例输出 #3
+
+```
+
+```
+
+## 提示
+
+![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF912D/40c8b1b61edb367e0e414618a2e0b777e6a3b2ba.png)
+
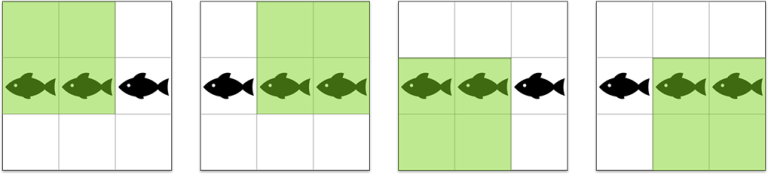
+对于30%的数据，$n,m\le 1000, r\le10, k\le 10^4$
+
+对于另20%的数据，$n,m\le 10^5, r\le10, k\le10$
+
+对于80%的数据，$n,m\le 10^5, r\le10, k\le 10^4$
+
+对于100%的数据，$1\le n,m\le 10^9, 1\le r\le 10, 1\le k\le 10^4$